 About this chapter
About this chapter


 About this chapter
About this chapter
|
 |
Strings

|
We begin our exploration of Ruby with the interactive Ruby shell
(irb). Open up a terminal and type:
irb --simple-prompt

|
Note:
Windows users will see a different command line: C:\>irb --simple-prompt >> |
Make sure that you can get irb working before you move on.
At the simplest level, you can use ruby as a calculator. Try this:
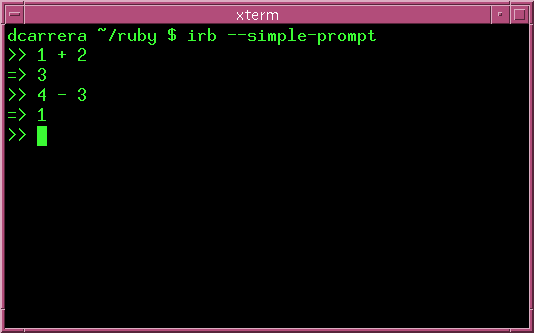
Ruby understands all the basic arithmetic operators that you would expect:
| Symbol | Meaning |
|---|---|
| + | addition |
| - | subtraction |
| * | multiplication |
| / | division |
To get out of irb type exit.

You should play around with these for a bit. Try this:

Notice what happens when you try to divide 3 by 2:
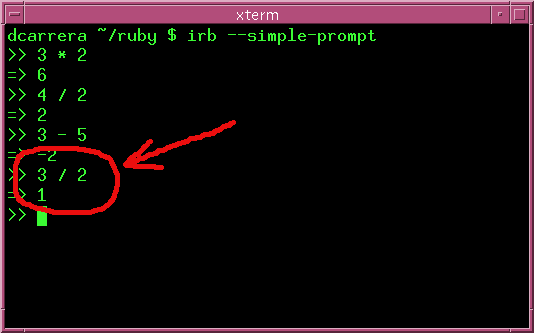
What happened? It turns out that Ruby understands two different classes of numbers:
An integer is a whole number, like 1, 2, -5, etc. When you operate using only integers, Ruby will give you an Integer answer.
3/2 is 1.5, but that is not an integer, so Ruby gives you 1 instead.
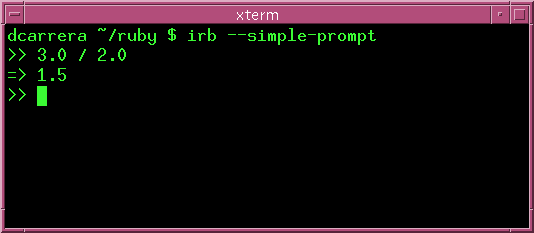
A float is a number with decimal places, like 3.14, 1.5, 3.0, etc. When you operate with Floats Ruby gives you a Float answer. For example:
Before we wrap up this chapter, let's look at two more operators:
| Symbol | Meaning |
|---|---|
| ** | exponent |
| % | remainder |

Notice how the remainder operator '%' behaves with decimals. In this example, 2 goes twice into 5.1 and there is 1.1 left over.
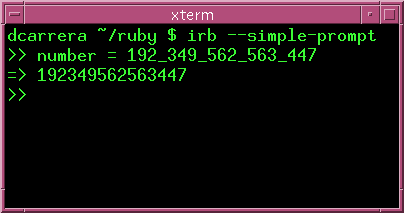
Ruby is good at dealing with very large and very small numbers. Suppose that you want to store the number 192349562563447.
Well, that's very hard to read. So, in English, you would normally write it as "192,349,562,563,447". Ruby uses something similar, using underscores:
What if you want 17_000_000_000_000_000_000 or 0.000_000_000_000_321? Normally you'd use scientific notation to write 1.7 x 1019 and 3.21 x 10-13. Again, Ruby gives you an alternative:
|
Note: The e stands for exponent, in the scientific notation. For example: 1.7e13 means 1.7 x 1013 2.1e-5 means 2.1 x 10-5 |
You can't "hurt" Ruby by giving it a number that is too large, but there are numbers that are too big for a computer to handle.
Once upon a time, a mathematecian called Edward Kasner asked his 9-year-old nephew, Milton Sirotta, to come up with a name for a really large number. The boy thought for a moment and then said... googol!. A googol is 10100 (that is, 1 followed by 100 zeroes).
Can you represent a googol with Ruby? Try typing this in irb:
googol = 10**100
|
Some time later, Dr. Kasner came up with a name for an even larger number, a googolplex. A googolplex is a 1 followed by googol zeroes. In other words, it is 10googol or 1010100. Can you represent a googolplex in Ruby? Try typing this in irb:
googolplex = 10**googol
|
How many hours are in a year?
How many minutes are in a decade?
How many seconds old are you?
What is 3.24 * ((34/2) - 54)/33.4 * 3.4?
Notice that you can use brackets (called parenthesis in US).
What do you think happens when you combine floats and integers? Try computing these:
Is the answer a float or an integer?
What is Infinity? One of the uses of the class Float is to represent numbers that might be too large or too small for an Integer. Try computing these in irb:
1/0
1.0/0
1/0.0
|
Notice that 1/0 gives you an error, and the others do not. Can you imagine why?
Type this on irb:
(1.0/0).is_a?(Integer)
(1.0/0).is_a?(Float)
|
What class is Infinity? Can you guess why 1/0 did not work in the previous exercise?
What would happen if you tried to represent a googolplex using Float's instead of Integer's? Type this in irb:
googol = 10.0 ** 100
googolplex = 10.0 ** googol
|
How is this different from when we used the Integer class?
A googolplex is a very large number, but is it infinite? Based on our experiments, how should we answer these questions:
 About this chapter
About this chapter
|
 |
Strings

|